JUNGLE_3주차
컴퓨팅 사고로의 전환 3주 차
주차별 키워드
- 그래프 탐색 기본, BFS, DFS, DFS(위상정렬)
더 고민해볼 키워드
- 벨만 포드 알고리즘
- SPFA
SW사관학교 정글 WEEK03 시험
- 단지 번호 붙이기 click
- 숨바꼭질 click
- 트리의 지름 click
트리의 지름
이번 주의 3번 문제였던 트리의 지름에 대해서 알아보자.
Tree(사이클이 없는 무방향 그래프)의 지름을 구하는 문제이다. 트리에서 어떤 두 노드를 선택해서 양쪽으로 쫙 당길 때, 가장 길게 늘어나는 경우가 있을 것이다. 이때 양끝을 이루는 두 노드 사이의 거리를 트리의 지름이라고 한다.
트리의 지름을 어떻게 구할 수 있을까?
아래의 방법으로 트리의 지름을 찾을 수 있다.
트리 내의 임의의 점 A로부터 가장 먼 점 B를 찾는다.
점 B로부터 가장 먼 점 C를 찾는다.
이때, B와 C사이의 거리가 트리의 지름이다.
어떻게 위의 방법이 반드시 성립할 수 있는지 알아보자.
- 트리의 지름을 이루는 양 끝 점을 u, v라고 하자.
- 임의의 점 A를 잡을 때, 아래의 3가지 경우가 가능하다.
1. 점 A가 u 혹은 v 인 경우
- u(=A)로부터 가장 먼 점은 v(=B)이고, u(=A)와 v(=B)사이의 거리가 트리의 지름이다.

2. 점 B가 u 혹은 v 인 경우
- A로부터 가장 먼 점은 B(=u)이다.
- u(=B)로부터 가장 먼 점은 v이고, u(=B)와 v사이의 거리가 트리의 지름이다.

3. A,B와 u,v가 다른 경우
- A로부터 가장 먼 점은 B이다.
- u로부터 가장 먼 점은 v이고, u와 v사이의 거리가 트리의 지름이다.
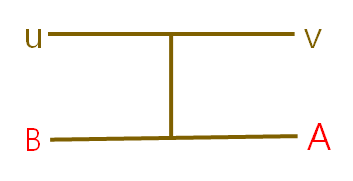
위의 경우들 중 3번 경우에는 아래의 가정이 틀리다는 것을 알 수 있다.
트리 내의 임의의 점 A로부터 가장 먼 점 B를 찾는다.
점 B로부터 가장 먼 점 C를 찾는다.
이때, B와 C사이의 거리가 트리의 지름이다.
따라서, 3번 경우가 없다는 것이 증명되면 위의 가정은 항상 참이라는 것을 보일 수 있다.
3번의 경우가 어떻게 존재할 수 없는지 알아보자.
3번 경우에서 A로부터 가장 먼 점은 B이고, u로부터 가장 먼 점은 v이다.
이때, u와 v사이의 거리가 트리의 지름이고, A,B,u,v는 겹치지 않는다.(모두 다른 점이다.)

A로부터 가장 먼 점이 B임으로, 아래와 같은 부등식이 성립한다.(d가 a+c보다 작으면 A로부터 가장 먼 점은 u가 되어야 함으로)
d > a + c
v로부터 가장 먼 점이 u임으로, 아래와 같은 부등식이 성립한다.
a > c + d
그런데, 두 부등식에는 모순이 있다.

문제에서 간선의 가중치는 양의 정수라고 명시되어 있음으로, 위의 부등식은 성립할 수 없다.
따라서, 3번과 같은 연결상태를 가지는 트리는 존재할 수 없고, 위의 가정이 참임을 알 수 있다!
구현
트리의 지름을 찾기 위해서는 A로부터 가장 먼 점 B, B로부터 가장 먼 점 C를 찾아야 한다.
각 점으로부터 가장 먼 점을 찾는 과정에서 djikstra알고리즘을 사용했다.
djikstra알고리즘에 대해서는 다른 포스팅에서 더 자세하게 설명하도록 하겠다.
Code
import sys
import heapq as hq
read=sys.stdin.readline
inf = sys.maxsize
n = int(read())
bridge = list([] for _ in range(n))
for _ in range(n-1):
a,b,c = map(int,read().split())
bridge[a-1].append((b-1,c))
bridge[b-1].append((a-1,c))
def dijkstra(v):
point = [(0,v)]
visit = list(inf for _ in range(n))
visit[v] = 0
while point:
prev_dist, prev_node = hq.heappop(point)
for next_node, next_dist in bridge[prev_node]:
if visit[next_node]> prev_dist+next_dist:
visit[next_node] = prev_dist+next_dist
hq.heappush(point,(visit[next_node],next_node))
return prev_dist, prev_node
print(dijkstra(dijkstra(0)[1])[0])
틀린 부분이 있을 수 있습니다. 피드백 주시면 고치도록 하겠습니다! 감사합니다.👍
[꼭 다시 풀어보기]