Python-6549-히스토그램에서 가장 큰 직사각형

히스토그램에서 가장 큰 직사각형 click

 

3달 전에 도전했다가 바로 포기했었던 문제이다. 이번에는 다행히 풀려서 기쁜 마음으로 포스팅한다. 

백준에서 처음으로 플레티넘 문제에서 정답을 받았다. 힌트도 없이!

 

문제 분석

 

높이가 다른 직사각형 여러 개로 이루어진 히스토그램이 주어졌을 때, 히스토그램에서 가장 넓이가 큰 직사각형을 구하는 문제이다.

 

직사각형들을 왼쪽에 위치하는 것 부터 차례대로 stack에 쌓아 나갔다.

stack에 직사각형의 높이 정보와 그 직사각형이 왼쪽으로 어디까지 이어질 수 있는지에 대한 정보를 저장했다.

히스토그램에서 가장 큰 직사각형

 

stack에는 직사각형의 높이 정보와 왼쪽으로 이어질 수 있는 최소의 index를 저장한다.

maxSize에는 직사각형의 최대 높이를 저장하고, 초기값은 0이다.

 

• 먼저 높이 2의 직사각형을 stack에 추가하자. 왼쪽으로 최대 0까지 이어질 수 있음으로, [2,0]이 추가된다.
• 다음 직사각형의 높이는 1이다. 높이 2인 직사각형은 더이상 오른쪽으로 이어질 수 없음으로, stack에서 pop한다. 이때 직사각형의 넓이는 2이고, maxSize를 2로 업데이트 한다.
• stack내에 1보다 작은 직사각형이 없음으로, 1을 stack에 추가해준다. 이 직사각형은 왼쪽으로 최대 0까지 이어질 수 있음으로, [1,0]이 추가된다. (0은 pop된 [2,0]으로부터 정보를 받아온 것이다.)

 

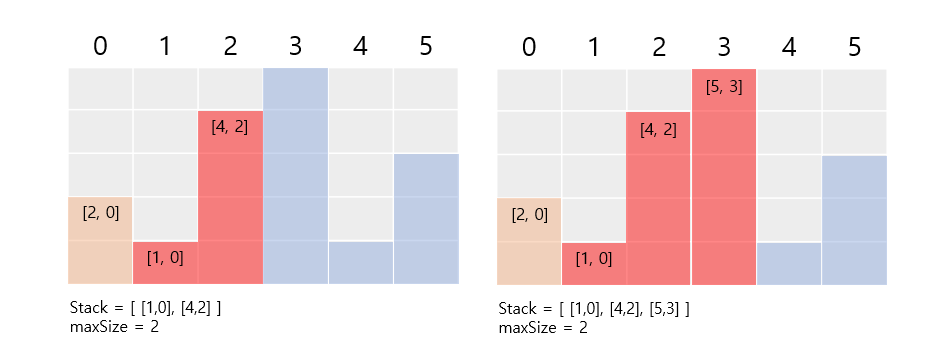
히스토그램에서 가장 큰 직사각형

 

• 직사각형의 높이는 4이다. stack내에 4보다 작거나 같은 직사각형이 없음으로, stack에 바로 추가해준다. 왼쪽으로 최대 2까지 이어질 수 있음으로, [4,2]를 추가한다.
• 직사각형의 높이는 5이다. stack내에 5보다 작거나 같은 직사각형이 없음으로, stack에 바로 추가해준다. 왼쪽으로 최대 3까지 이어질 수 있음으로, [5,3]를 추가한다.

 

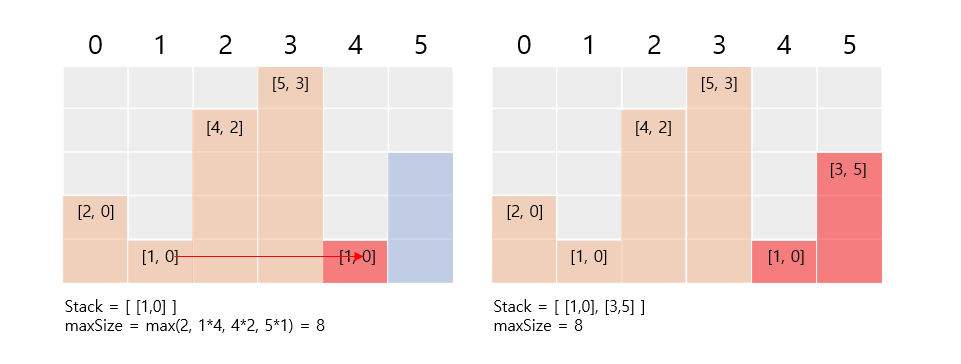
히스토그램에서 가장 큰 직사각형

 

• 다음 직사각형의 높이는 1이다. 5가 1보다 작거나 작음으로, stack에서 pop하고, maxSize를 갱신하자. maxSize = max(2, 5) = 5
• 4도 1보다 작거나 작음으로, stack에서 pop하고, maxSize를 갱신하자. maxSize = max(5, 8) = 8
• 1도 1보다 작거나 같음으로, stack에서 pop하고, maxSize를 갱신하자. maxSize = max(4, 8) = 8
• [1,0]으로부터 왼쪽으로 최대 이어질 수 있는 index를 전달받고, 높이와 함께 stack에 추가하자.

 

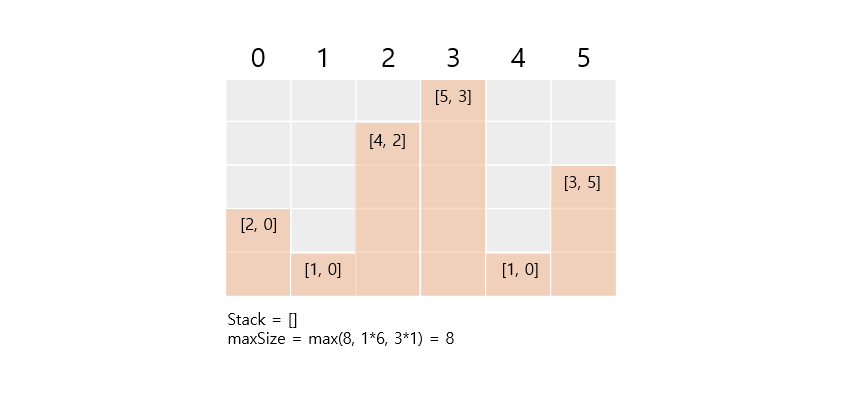
히스토그램에서 가장 큰 직사각형

• 직사각형을 모두 훑었다. 하지만 아직 Stack에는 pop되지 못한 직사각형들의 정보가 남아있다. 이들을 마저 꺼내서 업데이트 해주자.
• [3,5]는 최대 3 * (6-5) = 3의 넓이를 갖는다. [1,0]은 최대 1 * (6-0) = 6의 넓이를 갖는다. maxSize를 갱신하자.

이렇게 maxSize = 8을 얻을 수 있다!

 

 

Code

import sys
read=sys.stdin.readline

def maxSize():
    max_size = 0 #최대 넓이 저장
    stack = []

    for i in range(N):
        #왼쪽으로 이어질 수 있는 index
        min_point = i
        while stack and stack[-1][0] >= rect[i]:
            #pop되었다는 것은 추가 될 직사각형보다 높이가 높다는 의미이다.
            #따라서 추가될 직사각형은 pop되는 직사각형의 point값까지 넓어질 수 있다!
            #pop된 사각형의 point값으로 min_point를 업데이트
            h, min_point = stack.pop()
            tmp_size = h * (i-min_point)
            max_size = max(max_size, tmp_size)
        stack.append([rect[i],min_point])
    #탐색이 끝나고 아직 Stack에 남은 직사각형 정보로 maxSize 갱신
    for h, point in stack:
        max_size = max(max_size, (N-point)*h)

    return max_size

while True:
    N, *rect = map(int,read().split())
    if N == 0: 
        break
    print(maxSize())

 

틀린 부분이 있을 수 있습니다. 피드백 주시면 고치도록 하겠습니다! 감사합니다.👍

[꼭 다시 풀어보기]