Python-2098-외판원 순회

외판원 순회 click

 

2주일 전에 외판원 순회2를 풀고(외판원 순회2가 더 쉬운 난이도의 문제이다.) 도전해 봤는데, 실패했었다.

이번에는 DP와 비트마스킹을 사용해 풀어야한다는 사실을 인지하고, 풀었고, 칠판에 적으면서 2시간 가량 푼 끝에 정답을 맞출 수 있었다. 비트연산자를 사용해서 사고하기가 아직은 수월하지 않다는 생각이 들었다. 관련 문제들을 수요일까지 4문제 정도 더 풀어볼 예정이다.

 

 

 

문제 분석

 

비트마스크를 사용해 푸는 문제이다. 비트연산자를 다루는데 아직 익숙하지 않다면, 11723-집합 문제를 먼저 풀어보는 것을 추천한다.

 

1부터 N까지 번호가 매겨져 있는 도시들을 모두 거쳐 다시 원래의 도시로 돌아오는 최소 비용을 구하는 문제이다. 도시간에 이동하는데 드는 비용은 대칭적이지 않으며, 0으로 입력되어있는 경우, 이동할 수 없다는 뜻이다.

 

도시의 수는 최대 16으로, 비트마스킹을 이용한 DP로 풀어야만 해결할 수 있는 문제이다.

 

 

 

비트마스크 & DP

 

비트마스크를 사용해 현재까지 어떤 도시들을 방문했는지(0번 도시로부터 출발한다.) 저장했다. 이때, 동일한 도시들을 방문했더라도, 다른 도시에 있는 경우들이 있을 수 있다. 따라서 현재 도시의 정보도 저장해 주어야 한다.

 

[현재 도시] + [방문한 도시들의 정보(비트마스크)]로 이루어진 이차원 DP를 활용하자.

 

 

 

문제에서 주어진 예제 입력이다.

4
0 10 15 20
5 0 9 10
6 13 0 12
8 8 9 0

 

 

 

0번 도시를 시작으로 도시들을 순회할 계획이다.

한 바퀴를 순회할 것이기 때문에, 어느 도시에서 출발하더라도 결과는 같다.

0>1>2>3>0 으로 순회하는 것과, 1>2>3>0>1 으로 순회하는 방법의 비용은 동일하다.

 

도시의 수는 4개이고, 0번 도시를 제외한 우리가 방문할 도시는 3개이다. 방문한 도시들을 비트마스크에 저장할 예정임으로, (4-1) X 2^(4-1) [ 현재 도시 X 도시 방문 기록 ]의 크기를 가지는 DP배열을 만들어 주었다.

최소 비용을 갱신해 나가야 함으로 초기 값은 모두 무한대(sys.maxsize)로 설정해 주었다. 

 

• 110으로 표시된 칸의 경우 2번 도시와 3번 도시를 방문했다는 의미이다. 이진법으로 표기되어 있음으로, 실제 인덱스는 6이다.
• 101으로 표시된 칸의 경우 1번 도시와 3번 도시를 방문했다는 의미이다. 실제 인덱스는 5이다.

2차원 dp 배열

 

 

방문한 도시가 1개인 칸에 해당 도시까지 이동하며 든 비용을 입력한다. 

 

• dp[0][1 (= 001)] = 10
• dp[1][2 (= 010)] = 15
• dp[2][4 (= 100)] = 20

 

방문한 도시가 2개인 칸들도 해당 도시까지 이동하며 든 비용을 입력한다.

 

dp표의 왼쪽에 적힌 1,2,3은 도시의 번호이며, dp[][]로 표현할 때는 index로 넣었기 때문에 1번 도시는 0, 2번 도시는 1, 3번 도시는 2가 된다.

 

• dp[0][011] = dp[1][010] + 13 = 28
• dp[1][011] = dp[0][010] + 9 = 19
• ...

 

계속 이렇게 계산해 나갈 수는 없음으로 위의 경험을 바탕으로 점화식을 세워보자.

 

 

점화식

 

 

위의 방식을 컴퓨터에게 어떻게 알려줄 수 있을까?

'011'의 방문정보를 가지는 칸의 경우, 비트마스크를 이용해 탐색해야할 대상을 알 수 있다.

아래의 변수들을 이용해 점화식을 세워보자.

 

• i : 현재 방문한 도시들 ex) 001, 101, 110 ..
• v : 현재 도시
• j : 다음으로 방문할 도시

 

v 번 도시에서 한번 더 이동해 '011'의 방문정보를 가지기 위해서는 우선 v가 '011'내에 속해있어야 한다.

i = 011(2진법) = 3이라고 하면, 1<<(v-1) & i == True 을 만족하는 v에 대해서만 탐색하면 된다!  (도시가 1번 도시부터 n번 도시까지 존재하는데, 비트마스크를 사용할 때는 0번 도시부터 n-1번 도시로 생각해야 함으로, v에 1을 빼주어 사용했다.)

 

1<<(v-1) & i == True

 

 

탐색해야할 j는 어떻게 찾을 수 있을까?

j는 다음으로 방문할 도시이기 때문에, 현재 방문한 도시에 포함되면 안되며 v에서 j로 이동 가능해야 한다.

 

1<<(j-1) | i != i 

 

 

위의 두 조건을 만족하는 v와 j에 대해 아래의 점화식을 사용할 수 있다.

 

• dp[ j ][ 1<<(j-1) | i ] :  i도시들을 방문한 다음 j를 방문한 경우의 비용(다음 도시는 j이며, 다음 방문상태는 i와 j의 합집합이다.)
• dp[ v ][ i ] :  v에 위치하고, 현재 i도시들을 방문한 경우의 비용
• link[ v ][ j ] :  v도시로 부터 j도시까지 이동하는데 드는 비용

 

dp[ j ][ 1<<(j-1) | i ] = min(dp[ j ][ 1<<(j-1) | i ], dp[ v ][ i ]+link[ v ][ j ])

 

 

i에 저장되어 있는 도시들 + j를 방문했고, 현재 j에 위치하는 경우의 최소비용 보다 i에 저장되어 있는 도시들을 방문했고, 현재 v에 위치하는 경우의 최소비용 + v로부터 j까지 이동하는데 드는 비용이 적다면, 업데이트 해준다.

 

점화식 활용

 

점화식을 i = 001(이진법) = 1 인 경우, 다음 도시를 방문할 때 드는 비용을 구하는데 활용해보자.

 

 

 

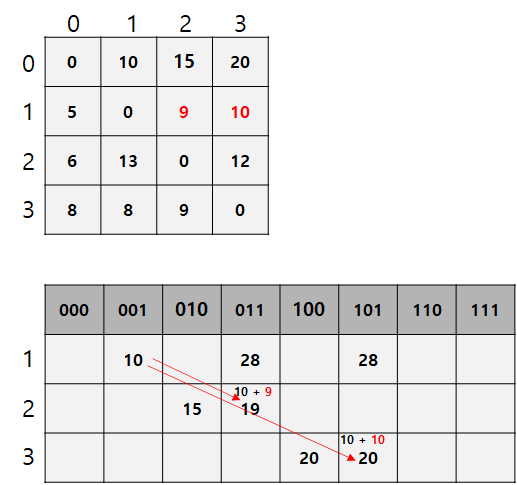
• i : 현재 방문한 도시들
• v : 현재 도시
• j : 다음으로 방문할 도시

 

i = 001(이진법) = 1이다.

현재 도시로 가능한 v 값은 1이다.

다음으로 방문 가능한 도시 j 는 2와 3이다. 

 

• dp[1][011] = dp[0][001] + 9 = 28
• dp[2][101] = dp[0][001] + 10 = 19

 

이렇게 가능한 모든 dp값을 채우자. 

 

 

 

 

 

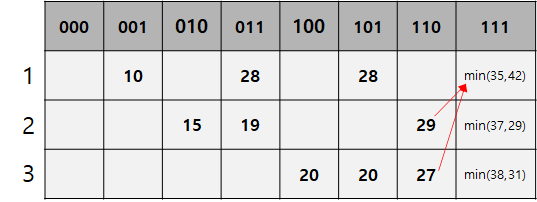
이렇게 i = 111인 경우의 값을 모두 얻었다.

i = 111인 경우, 0에서 출발해 1,2,3번 도시를 모두 돌았다는 뜻이다.

이제 0으로 다시 돌아가야 함으로, 각 도시에서 0번 도시로 이동하는 경비를 더해 최솟값을 구할 수 있다!

 

Code

import sys
read=sys.stdin.readline
inf = sys.maxsize

def TSP():
    dp = list(list(inf for _ in range(2**(n-1))) for _ in range(n))
    for i in range(n):
        dp[i][0] = 0
        if link[0][i]: 
            dp[i][1<<(i-1)] = link[0][i]

    for i in range(1,2**(n-1)):
        for v in range(1,n):
            if 1<<(v-1) & i:
                for j in range(1,n):
                    if 1<<(j-1)|i != i and link[v][j]!=0:
                            dp[j][1<<(j-1)|i] = min(\
                                dp[j][1<<(j-1)|i],\
                                dp[v][i]+link[v][j]\
                                )

    print(min(list(dp[i][-1]+link[i][0] for i in range(n) if dp[i][-1]!=inf and link[i][0])))
    

n = int(read())
link = list(list(map(int,read().split())) for _ in range(n))

TSP()

 

틀린 부분이 있을 수 있습니다. 피드백 주시면 고치도록 하겠습니다! 감사합니다.👍

[꼭 다시 풀어보기]