B-Tree - 삽입

이번 포스팅에서는 트리를 단순화하기 위해, 키와 관련된 부수적인 정보는 키와 같은 노드에 있다고 가정한다.

 

Abdul Bari 교수님의 10.2 B Trees and B+ Trees. How they are useful in Databases click 

위의 강의에서 설명하는 방식과 다른 방식의 삽입을 설명합니다.

해당 포스팅에서 설명하는 방식은 루트 노드에서 리프 노드까지 Top-Down으로 내려가며 재귀적으로 탐색하는 방식입니다.

 

 

B-Tree - 기본 규칙

 

 

B Tree 예시 (ref- programize)

 

1. 모든 노드 x는 아래와 같은 속성이 있다.
    a. x.n은 노드 x에 현재 저장되어 있는 키의 개수다.
    b. x의 key들은 x.key(1) <= x.key(2) <= ... <= x.key(x.n) 이 되도록 단조증가하는 순서로 정렬되어 있다.
    c. x가 리프 노드일 때는 x.leaf가 1이며, x가 내부 노드일 때는 x.leaf가 0이다.
2. 각 내부 노드 x는 리프 노드가 아닐 때 자식 노드를 가리키는 x.n+1개의 포인터 x.c(1), x.c(2), ... x.c(x.n+1)를 가진다. 자식 노드의 개수는 항상 키의 개수 + 1이다.
3. x.key(i)는 각 서브 트리에 저장되는 키들의 범위를 분할한다. x.key(i)는 x.c(i)의 key들보다 항상 크고, x.c(i+1)의 key들보다 항상 작다.
4. 모든 리프 노드는 트리 높이 h와 같은 깊이를 가진다.
5. 노드는 그들이 포함할 수 있는 키의 개수에 대해 상한과 하한을 가진다. 이런 한계를 B-Tree의 최소 차수라고 하는 일정한 정수 T>=2를 이용해 포현한다.
    a. 루트를 제외한 모든 노드는 t-1개 이상의 키를 가진다. 따라서, 루트 노드를 제외한 모든 내부 노드는 자식 노드를 적어도 t개 가진다. 트리가 비지 않았다면, 루트는 키를 적어도 하나 가진다.
    b. 모든 노드는 2t-1개 이하의 키를 가진다. 따라서, 하나의 내부 노드에는 자식 노드를 최대 2t개 가진다. 키를 정확히 2t-1개 가지는 경우 해당 노드를 가득 차 있다고 한다.

 

 

1~5번 규칙들은 책에 있는 내용을 그대로 옮겨온 것이다. 이 문장들을 조금 더 자세히 살펴보자.

 

 

 

내부 노드 & 리프 노드

 

리프노드는 트리의 가장 아래 위치하는 노드이다. 따라서, 리프 노드에는 자식 노드(x.child)가 존재하지 않는다.

위의 그림에서 각 노드는 5개의 key를 가지기 때문에 x.n = 5이다.

내부 노드의 경우 5개의 key를 가지고, key의 개수보다 1이 많은 6개의 자식을 '반드시' 가진다.

B Tree에서는 노드 내에 들어갈 수 있는 key 개수의 범위가 제한되어 있다. 만약 차수(t)가 3이라면, 노드에 들어갈 수 있는 키 개수의 최대값은 5개(2t-1)이고, 최소값은 2개(t-1)이다. 

 

 

 

t=3인 경우 노드에 들어갈 수 있는 키 개수의 최대값과 최소값

 

차수가 3인 경우 노드의 키 개수가 5이면, 노드의 키 개수가 최대이고, 노드의 키 개수가 2이면, 노드의 키 개수가 최소이다. 노드에 들어갈 수 있는 키 개수의 범위가 제한되어 있다는 사실은 굉장히 중요하다. 

 

 

 

 

삽입을 할 때, 노드의 키 개수가 이미 최대라면 더 이상 삽입할 수 없음으로, 해당 노드를 분할한 후에 삽입해야 한다. 

이렇게 노드를 분할할지 말지에 대한 기준이 되는 숫자가 2t-1이다. 분할된 노드의 키의 개수는는 각각 t-1개 t-1개이며, 중간값을 가지는 키 1개가 부모노드로 올가가게 된다.

 

* t-1은 삭제시 노드를 병합해야할지 말지에 대한 기준이 되는 숫자이고 뒤에서 다음 포스팅에서 다시 다룰 예정이다. 우선은 삭제 과정에 집중하자.

 

 

 

 

 

B-Tree - 삽입

 

B Tree에서는 단순히 키가 삽입될 리프 위치를 찾아 삽입할 수 없다. 왜냐하면 삽입 후의 결과가 조건에 모두 부합하는 올바른 B Tree가 되지 않을 가능성이 있기 때문이다. (삽입 되어야 할 위치에 이미 2t-1개의 노드가 존재한다면, 1개의 키가 추가되는 순간 조건에 위배된다.)

따라서, 루트 노드에서 리프 노드 방향으로 키가 삽입될 위치를 찾아가면서, 경로에 존재하는 키의 개수가 (2t-1)개인 가득 찬 노드들을 미리 분할한다. 이 과정을 통해 리프 노드에 도달하게 되면 가득 찬 노드를 분할하고자 할 때마다 그 부모가 가득 차 있지 않음이 보장된다. 또한, 리프 노드에 도달했을 때, 리프노드 또한 가득 차 있지 않음이 보장된다.

 

 

 

1. 분할

 

 

 

 

 

위의 그림과 같이 자식 노드가 분할되어 중간값 6이 부모 노드로 올라온다. 

이때, 부모 노드에 6이 추가되기 전에 존재하던 키의 개수가 2t-1개였다면, 6이 들어옴으로써 키의 개수가 2t개가 되고 이는 범위를 초과하기 때문에 다시 부모노드를 분할해 주어야 한다. 이 과정이 연쇄적으로 발생할 수 있기 때문에, 이를 미연에 방지하고자 우리가 이동하는 경로에서 만나는 노드의 키의 개수가 2t-1개라면, 미리 모두 분할해 주었다.

 

우리가 이동할 노드의 키가 2t-1개일 때, 해당 노드를 분할하며 내려갈 것이다.

위의 방식으로 리프 노드에 도달하게 되면 가득 찬 노드를 분할하고자 할 때마다 그 부모가 가득 차 있지 않음이 보장된다. 

 

 

 

• 분할 과정

 

아래의 그림과 같이 node x 가 존재하고, 키가 내려갈 node는 y라고 하자. y에 존재하는 키의 개수가 2t-1개라면, y를 분할한 후에 k를 y로 내려보내야 한다. y를 분할하는 과정이 어떻게 이루어지는지 조금 더 자세히 알아보자.

 

 

 

분할하기 위해 분할된 값들이 들어갈 node를 추가로 생성하고, 이 노드를 z라고 하자.

 

 

 

 

y를 분할하면, 키 1개가 x로 올라가게 된다. 이 키가 들어갈 자리를 확보하기 위해 x의 키를 오른쪽으로 한 칸씩 오른쪽으로 밀어준다. 그림에서는 나타내지 않았지만, x에는 자식들을 가리키는 포인터들도 존재한다. x에서 z를 가리킬 포인터를 y 오른쪽에 삽입해 주어야 함으로, 이 공간을 확보하기 위해 x의 자식들도 한 칸씩 오른쪽으로 밀어준다.

 

 

 

 

 

공간이 확보되었음으로, y의 키들을 노드 x와 z에 각각 분할해주자.

 

 

 

 

 

이제 k를 자식 노드로 내려보내야 한다. 그런데, y.key2가 y로부터 x로 올라왔음으로, k가 y.key2보다 큰지 작은지 한번 더 확인해주어야 한다. k가 y.key2보다 크다면, i+1번째 자식으로, 그렇지 않다면 그대로 i번째 자식으로 내려보내면 된다.

 

 

Code - B_Tree_Split_child

void B_Tree_Split_Child(node* x, int i)
{
	node* z = malloc(sizeof(node));
	if (z == NULL)
	{
		printf("memory allocation falied");
		return;
	}
	node* y = x->child[i]; // 0 <= i
	z->leaf = y->leaf;
	z->n = DEGREE - 1;
	for (int j = 0; j < DEGREE - 1; j++)
	{
		z->key[j] = y->key[j + DEGREE];
	}
	if (y->leaf == FALSE)
	{
		for (int j = 0; j < DEGREE; j++)
		{
			z->child[j] = y->child[j + DEGREE];
		}
	}
	y->n = DEGREE - 1;
	for (int j = x->n; j > i; j--)
	{
		x->child[j + 1] = x->child[j];
	}
	x->child[i + 1] = z;
	for (int j = x->n - 1; j > i - 1; j--)
	{
		x->key[j + 1] = x->key[j];
	}
	x->key[i] = y->key[DEGREE - 1];
	x->n = x->n + 1;
}

 

 

 

2. 키 삽입

 

내부 노드에는 키가 삽입될 수 없다.

 

B Tree에서 키는 리프 노드에서만 삽입된다.

 

리프 노드를 제외한 모든 노드에 n개의 키가 존재할 때, 자식은 n+1개 존재해야 한다. 리프 노드에는 자식이 존재하지 않기 때문에, 키를 한 개 더 추가하더라도 규칙에 위배되지 않는다. 하지만, 자식을 가지고 있는 내부 노드에 키를 추가하게 되면, 자식의 수와 키의 개수가 동일해지고, 트리의 규칙에 위배된다. 따라서, 키는 리프 노드에서만 삽입될 수 있다.

 

 

Code - B_Tree_Insert_Nonfull

void B_Tree_Insert_Nonfull(node* x, int k)
{
	int i = x->n;

	if (x->leaf)
	{
		i--;
		while (i >= 0 && k < x->key[i])
		{
			x->key[i + 1] = x->key[i];
			i--;
		}
		x->key[i + 1] = k;
		x->n = x->n + 1;
	}
	else {
		while (i >= 1 && k < x->key[i - 1])
		{
			i--;
		}
		if ((x->child[i])->n == 2 * DEGREE - 1)
		{
			B_Tree_Split_Child(x, i);
			if (k > x->key[i]) {
				i++;
			}
		}
		//printf("child#: %d k: %d\n", i, k);
		B_Tree_Insert_Nonfull(x->child[i], k);
	}
}

 

 

3. 예외 상황(분할)

 

 

 

x가 루트 노드인 경우, 1번과 같이 분할할 수 없다.

 

x가 루트 노드라면, x의 부모 노드는 존재하지 않는다는 뜻이다. 이때, 분할한 값을 담을 노드 z를 생성하고, 1번과 같이 분할 과정을 진행하게 되면, x.key2가 갈 곳이 없다는 문제가 생긴다.

 

 

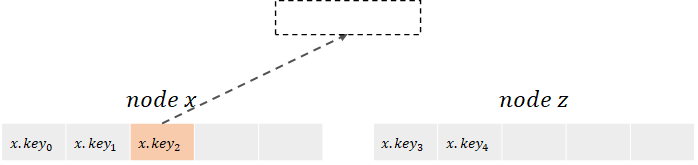
따라서, x가 루트 노드인 경우에는 x의 중간값이 올라갈 새로운 루트 노드를 하나 생성한 후에, 1번과 같은 과정을 진행해 주어야 한다.

 

 

위의 경우를 예외적으로 처리하기 위해서, B_Tree_Insert함수와, B_Tree_Insert_main함수로 나누어 작성해 주었다.

 

B_Tree_Insert함수는 루트 노드를 확인한 후에 위의 경우와 같이 가득 차있으면, split되었을 때, 중간값이 올라갈 수 있는 빈 노드를 형성시키고, B_Tree_Split_child 함수를 실행하게 된다. 이후 노드 부터는 B_Tree_Split_child와 B_Tree_Insert_Nonfull함수가 재귀적으로 처리하며 내려가게 된다.

 

Code

void B_Tree_Insert(B_Tree* T, int k)
{
	node* r = T->root;
	if (r->n == 2 * DEGREE - 1)
	{
		node* s = malloc(sizeof(node));
		if (s == NULL) {
			printf("memory allocation falied");
			return;
		}
		T->root = s;
		s->leaf = FALSE;
		s->n = 0;
		s->child[0] = r;
		B_Tree_Split_Child(s, 0);
		B_Tree_Insert_Nonfull(s, k);
		//printf("insert %d\n", k);
	}
	else
	{
		B_Tree_Insert_Nonfull(r, k);
	}
}

 

 

 

---

위의 조건들을 생각하며, B Tree에 원소k 가 삽입되는 경우에 대해 생각해보자.

 

 

 

1. node x가 리프 노드이면, x에 원소k를 삽입한다.

x 가 리프노드인 경우

 

 

2. node x가 리프 노드가 아닌 경우 원소k를 자식 노드로 내려준다. 이때, 원소k가 내려가게 될 자식 노드(y)를 사전에 체크해 주어야 한다.

 

• 2 - 1. y가 가진 키의 개수가 2t-1개 보다 적다면, 키가 추가로 삽입될 공간이 존재함으로 재귀 함수를 호출해 y로 k를 보내준다.

y의 키 개수가 2t-1보다 작은 경우

 

• 2 - 2. y가 가진 키의 개수가 2t-1개 라면, 키가 추가로 삽입될 공간이 없음으로, y를 먼저 분할한다. 이때, y가 분할되며, 키 1개가 x로 올라오게 되는데, x는 이미 2t-1개 미만의 키를 가지는 것이 보장되어 있음으로, y로부터 1개의 키가 x로 올라오더라도 x의 키의 개수는 2t-1개를 초과하지 않는다.

y가 분할되고, y의 중간값이 x로 올라온다. 이때, x는 2t-1개보다 적은 수의 키를 가지고 있음으로, 키가 추가로 삽입될 수 있음이 보장된다.

 

k가 y.key2보다 큰지 작은지에 따라서, 2번 child로 내려갈지, 3번 child로 내려갈지가 결정된다. k와 y.key2를 비교해 재귀함수를 실행시키자.

 

 

 

 

 

Code 

/*
 * Btree example
 *
 *
 * 20210109, youseop, jeongseo, gojae
 *
 *
 */
 /*
  *
  * 1.	모든 리프노드는 트리 높이(h)와 같은 깊이에 있다.
  * 2.	t-1 <= 키의 개수 <= 2t-1
  * 2-1	루트 노드의 키의 개수는 t-1개 보다 적을 수 있다.
  * 3.	리프 노드가 아닐 경우, 키의 개수 +1개 = 자식의 개수 <= 2t
  *
  */
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
#define EMPTY 0
#define DEGREE 2 /*The degree of the tree.*/


typedef struct node
{
	int key[2 * DEGREE - 1];
	struct node* child[2 * DEGREE];
	int leaf;
	int n;
}
node;


typedef struct B_Tree
{
	node* root;
}B_Tree;


void B_Tree_Create(B_Tree* T);
void B_Tree_Insert(B_Tree* T, int k);
void B_Tree_Insert_Nonfull(node* x, int k);
int  B_Tree_Search(B_Tree* T, int k);
int  B_Tree_Search_Main(node* x, int k);
void B_Tree_Split_Child(node* x, int i);
void B_Tree_Display(B_Tree* T);
void B_Tree_Display_Main(node* x, int h);
void B_Tree_Delete(B_Tree* T, int k);
void B_Tree_Delete_main(node* x, int k);
int Find_Successor(node* x);
int Find_Predecessor(node* x);

void B_Tree_insert_items(B_Tree* T, int x, int y);


void main()
{
	B_Tree* T = malloc(sizeof(B_Tree));
	B_Tree_Create(T);
	xx->child[1] = z;

	int command, x, y;
	printf("##########################\n\n    $ B_TREE Project $ \n\nproduced by \n\n@jeongseo \n@youseop \n@gojae\n\n##########################\n\n");
	while (1) {
		printf("\n1: insert one item\n2: insert items (x~y)\n3: delete item\n4: display\ncommad: ");
		scanf("%d", &command);
		if (command == 1) {
			printf("insert item: ");
			getchar();
			scanf("%d", &x);
			B_Tree_Insert(T, x);
			B_Tree_Display(T);
		}
		else if (command == 2) {
			printf("\ninsert x & y\n (y should be bigger than x)\nx: ");
			getchar();
			scanf("%d", &x);
			printf("y: ");
			getchar();
			scanf("%d", &y);
			B_Tree_insert_items(T, x, y);
		}
		else if (command == 3) {
			printf("\ninsert a number you wanna delete.\nk : ");
			getchar();
			scanf("%d", &x);
			B_Tree_Delete(T, x);
			B_Tree_Display(T);
		}
		else if (command == 4) {
			B_Tree_Display(T);
		}
		else if (command == 0) {
			break;
		}
		getchar();
	}

	free(T);
}


void B_Tree_insert_items(B_Tree* T, int x, int y) {
	for (int i = x; i < y + 1; i++) {
		B_Tree_Insert(T, i);
	}
	B_Tree_Display(T);
}



void B_Tree_Create(B_Tree* T)
{
	node* x = malloc(sizeof(node));
	if (x == NULL) {
		printf("memory allocation falied");
		return;
	}
	x->leaf = TRUE;
	x->n = 0;
	T->root = x;
}


void B_Tree_Insert(B_Tree* T, int k)
{
	node* r = T->root;
	if (r->n == 2 * DEGREE - 1)
	{
		node* s = malloc(sizeof(node));
		if (s == NULL) {
			printf("memory allocation falied");
			return;
		}
		T->root = s;
		s->leaf = FALSE;
		s->n = 0;
		s->child[0] = r;
		B_Tree_Split_Child(s, 0);
		B_Tree_Insert_Nonfull(s, k);
		//printf("insert %d\n", k);
	}
	else
	{
		B_Tree_Insert_Nonfull(r, k);
	}
}


void B_Tree_Insert_Nonfull(node* x, int k)
{
	int i = x->n;

	if (x->leaf)
	{
		i--;
		while (i >= 0 && k < x->key[i])
		{
			x->key[i + 1] = x->key[i];
			i--;
		}
		x->key[i + 1] = k;
		x->n = x->n + 1;
	}
	else {
		while (i >= 1 && k < x->key[i - 1])
		{
			i--;
		}
		if ((x->child[i])->n == 2 * DEGREE - 1)
		{
			B_Tree_Split_Child(x, i);
			if (k > x->key[i]) {
				i++;
			}
		}
		//printf("child#: %d k: %d\n", i, k);
		B_Tree_Insert_Nonfull(x->child[i], k);
	}
}


int B_Tree_Search(B_Tree* T, int k)
{
	node* r = T->root;
	return B_Tree_Search_Main(r, k);
}

//함수 수정 필요!
int B_Tree_Search_Main(node* x, int k)
{
	if (x->leaf)
	{
		int i = x->n - 1;
		while (i >= 0 && k < x->key[i])
		{
			i--;
		}
		if (x->key[i] == k)
		{
			printf("There is data\n");
			return TRUE;
		}
		else
		{
			printf("No data\n");
			return FALSE;
		}
	}
}


void B_Tree_Split_Child(node* x, int i)
{
	node* z = malloc(sizeof(node));
	if (z == NULL)
	{
		printf("memory allocation falied");
		return;
	}
	node* y = x->child[i]; // 0 <= i
	z->leaf = y->leaf;
	z->n = DEGREE - 1;
	for (int j = 0; j < DEGREE - 1; j++)
	{
		z->key[j] = y->key[j + DEGREE];
	}
	if (y->leaf == FALSE)
	{
		for (int j = 0; j < DEGREE; j++)
		{
			z->child[j] = y->child[j + DEGREE];
		}
	}
	y->n = DEGREE - 1;
	for (int j = x->n; j > i; j--)
	{
		x->child[j + 1] = x->child[j];
	}
	x->child[i + 1] = z;
	for (int j = x->n - 1; j > i - 1; j--)
	{
		x->key[j + 1] = x->key[j];
	}
	x->key[i] = y->key[DEGREE - 1];
	x->n = x->n + 1;
}


void B_Tree_Display(B_Tree* T)
{
	node* r = T->root;
	B_Tree_Display_Main(r, 1);
}


void B_Tree_Display_Main(node* x, int h)
{
	printf("%d : ", h);
	for (int i = 0; i < x->n; i++)
	{
		printf("%d ", x->key[i]);
	}
	printf("\n");
	if (x->leaf == 0)
	{
		for (int i = 0; i < x->n + 1; i++)
		{
			B_Tree_Display_Main(x->child[i], h + 1);
		}
	}
}


void B_Tree_Delete(B_Tree* T, int k)
{
	node* r = T->root;
	int i = r->n - 1;
	if (r->leaf == 1)
	{
		while (i >= 0 && r->key[i] > k)
		{
			i--;
		}
		if (i >= 0 && r->key[i] == k) {
			for (int j = i + 1; j < r->n; j++)
			{
				r->key[j - 1] = r->key[j];
			}
			r->n--;
			printf("delete success\n");
		}
		else {
			printf("no data");
		}
		return;
	}
	else {
		if (r->n > 1) {
			B_Tree_Delete_main(r, k);
		}
		else {
			node* left_c = r->child[0];
			node* right_c = r->child[1];
			if (left_c->n == DEGREE - 1 && right_c->n == DEGREE - 1) {
				left_c->key[DEGREE - 1] = r->key[0];
				for (int j = 0; j < DEGREE - 1; j++) {
					left_c->key[DEGREE + j] = right_c->key[j];
				}
				if (left_c->leaf == FALSE) {
					for (int j = 0; j < DEGREE; j++) {
						left_c->child[DEGREE + j] = right_c->child[j];
					}
				}
				left_c->n = DEGREE * 2 - 1;
				free(right_c);
				T->root = left_c;
				free(r);
				B_Tree_Delete_main(left_c, k);
			}
			else {
				B_Tree_Delete_main(r, k);
			}
		}
	}
}


void B_Tree_Delete_main(node* x, int k) {
	printf("star %d\n", k);
	int i = x->n;
	while (i > 0 && x->key[i - 1] >= k) {
		i--;
	}
	if (i < x->n && x->key[i] == k) {
		if (x->leaf == 1) {
			for (int j = i; j < x->n - 1; j++) {
				x->key[j] = x->key[j + 1];
			}
			x->n--;
			return;
		}
		else {
			printf("no leaf\n");
			node* left_c = x->child[i];
			node* right_c = x->child[i + 1];
			if (left_c->n > DEGREE - 1) {
				printf("here?\n");
				int pre_k = Find_Predecessor(left_c);
				printf("%d\n", pre_k);
				x->key[i] = pre_k;
				B_Tree_Delete_main(left_c, pre_k);
			}
			else if (right_c->n > DEGREE - 1) {
				int su_k = Find_Successor(right_c);
				x->key[i] = su_k;
				B_Tree_Delete_main(right_c, su_k);
			}
			else {
				left_c->key[DEGREE - 1] = k;
				for (int j = 0; j < DEGREE - 1; j++)
				{
					left_c->key[DEGREE + j] = right_c->key[j];
				}
				for (int j = 0; j < DEGREE; j++) {
					left_c->child[DEGREE + j] = right_c->child[j];
				}
				left_c->n = 2 * DEGREE - 1;
				for (int j = i; j < x->n - 1; j++) {
					x->key[j] = x->key[j + 1];
				}
				for (int j = i + 1; j < x->n; j++) {
					x->child[j] = x->child[j + 1];
				}
				x->n--;
				free(right_c);
				B_Tree_Delete_main(left_c, k);
			}
		}
	}
	else
	{
		node* my_way_c = x->child[i];
		if (my_way_c->n > DEGREE - 1)
		{
			B_Tree_Delete_main(my_way_c, k);
		}
		else
		{
			if (i != 0 && (x->child[i - 1])->n > DEGREE - 1)
			{
				node* left_c = x->child[i - 1];
				for (int j = DEGREE - 2; j >= 0; j--) {
					left_c->key[j + 1] = left_c->key[j];
				}
				if (left_c->leaf == FALSE)
				{
					for (int j = DEGREE - 1; j >= 0; j--) {
						left_c->child[j + 1] = left_c->child[j];
					}
				}
				my_way_c->key[0] = x->key[i - 1];
				my_way_c->child[0] = left_c->child[left_c->n];
				my_way_c->n++;
				x->key[i - 1] = left_c->key[left_c->n - 1];
				left_c->n--;
			}
			else if (i != x->n && (x->child[i + 1])->n > DEGREE - 1)
			{
				node* right_c = x->child[i + 1];
				my_way_c->key[DEGREE - 1] = x->key[i];
				my_way_c->child[DEGREE] = right_c->child[0];
				my_way_c->n++;
				x->key[i] = right_c->key[0];
				for (int j = 0; j < right_c->n - 1; j++)
				{
					right_c->key[j] = right_c->key[j + 1];
				}
				for (int j = 0; j < right_c->n; j++) {
					right_c->child[j] = right_c->child[j + 1];
				}
				right_c->n--;
			}
			else {//x에 k가 없고, 풍족한 형제가 없을때!!!
				if (i == 0) {
					node* right_c = x->child[i + 1];
					for (int j = 0; j < DEGREE - 1; j++) {
						right_c->key[j + DEGREE] = right_c->key[j];
						right_c->key[j] = my_way_c->key[j];
					}
					if (right_c->leaf == 0) {
						for (int j = 0; j < DEGREE; j++) {
							right_c->child[j + DEGREE] = right_c->child[j];
							right_c->child[j] = my_way_c->child[j];
						}
					}
					right_c->key[DEGREE - 1] = x->key[i];
					right_c->n = DEGREE * 2 - 1;
					for (int j = 0; j < x->n - 1; j++) {
						x->key[j] = x->key[j + 1];
					}
					for (int j = 0; j < x->n; j++)
					{
						x->child[j] = x->child[j + 1];
					}
					free(my_way_c);
					my_way_c = right_c;
					x->n--;
				}
				else {
					node* left_c = x->child[i - 1];
					left_c->key[DEGREE - 1] = x->key[i - 1];
					for (int j = 0; j < DEGREE - 1; j++) {
						left_c->key[j + DEGREE] = my_way_c->key[j];
					}
					if (left_c->leaf == 0) {
						for (int j = 0; j < DEGREE; j++) {
							left_c->child[j + DEGREE] = my_way_c->child[j];
						}
					}
					left_c->n = 2 * DEGREE - 1;
					for (int j = i - 1; j < x->n - 1; j++) {
						x->key[j] = x->key[j + 1];
					}
					for (int j = i; j < x->n; j++) {
						x->child[j] = x->child[j + 1];
					}
					free(my_way_c);
					my_way_c = left_c;
					x->n--;
				}
			}
			B_Tree_Delete_main(my_way_c, k);
		}
	}
	return;
}

int Find_Predecessor(node* x) {
	while (x->leaf == 0) {
		x = x->child[x->n];
	}
	return x->key[x->n - 1];
}

int Find_Successor(node* x) {
	while (x->leaf == 0) {
		x = x->child[0];
	}
	return x->key[0];
}